基础数据结构分析汇总

数据结构与算法

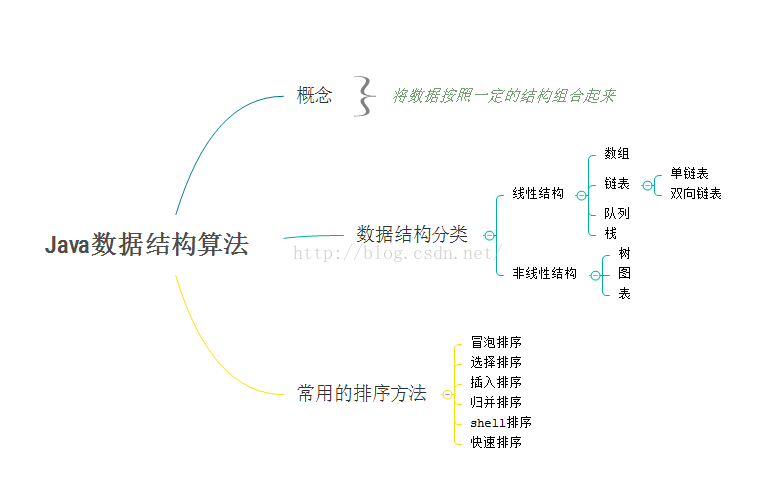
数据结构是计算机存储、组织数据的方式。数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。通常情况下，精心选择的数据结构可以带来更高的运行或者存储效率。

数据结构与算法学习大纲

数组

特点：元素在内存中线性连续存储，可以根据下标快速访问数组元素，但是增删效率不是很高，每一次增加或删除元素都需要
大量移动元素空出插入位置或者填补删除元素的位置。
使用场景：频繁查询，很少进行增加或删除操作的情况

1
2
3
4
5
6
7
8
9
10
11
//声明
int a[];
int c[] = new int[]{1,3,4,5,6};
//申请空间，int数组默认初始值为0
a= new int[5];
//根据下标单个赋值初始化
a[0] = 2;
//循环赋值
for (int i = 0; i < a.length; i++) {
    a[i] = i;
}

java中对数组的排序有两种方法，第一种是直接使用Arrays API中的sort(Object[] a)方法进行排序或者采用算法中的
各类算法，比如：冒泡排序，选择排序，插入排序，归并排序等等。

队列

特点：先进先出(FIFO/fisrt in first out),如同一个单向隧道，先进的车先出。
使用场景：多线程的阻塞队列管理非常有用

  • 数组实现自定义队列

(1)自定义队列接口CustomQueue.java

1
2
3
4
5
6
7
8
9
10
11
12
public interface CustomQueue<T> {
    //入队函数，实现队列添加元素
    public void put(T data)throws Exception;
    //出队函数，实现队列元素删除
    public T remove()throws Exception;
    //判断是否队列为空
    public boolean isEmpty();
    //获取队列的长度
    public int size();
    //获取队列队头元素
    public T getFrontElement()throws Exception;
}

(2)数组实现对列自定义类CustomArrayQueue.java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
public class CustomArrayQueue<T> implements CustomQueue<T> {
    //默认队列长度
    static final int defaultSize = 15;
    //队列元素集合
    private T[] queueVals;
    //队列长度
    private int size;
    //队列第一个对象的位置
    private int front;
    //队列当前对象的位置
    private int rear;
    /*
     *默认构造方法，设置默认队列长度为15
     */
    @SuppressWarnings("unchecked")
    public CustomArrayQueue (){
        front=rear=0;
        size = 0;
        queueVals = (T[]) new Object[defaultSize];
    }
    /*
     *带参构造方法，队列长度可自定义
     */
    @SuppressWarnings("unchecked")
    public CustomArrayQueue (int defineSize){
        front=rear=0;
        size = 0;
        queueVals = (T[]) new Object[defineSize];
    }
    /*
     *添加对象到队列中
     */
    @Override
    public void put(T data) throws Exception {
        if (size>0 && front==rear) {
            throw new Exception("队列已经满辣！");
        }else {
            queueVals[rear] = data;
            rear =(rear+1)%(queueVals.length);
            size++;
        }
    }
    /*
     *从队列中队首元素
     */
    @Override
    public T remove() throws Exception {
        T object = null;
        if (isEmpty()) {
            throw new RuntimeException("队列什么也没有啦！");
        }else {
            //获取队首对象元素
            object = queueVals[front];
            //将队首元素置为null
            queueVals[front] = null;
            front =(front+1)%(queueVals.length);
            size--;
        }
        return object;
    }
    /*
     *判断队列是否为空
     */
    @Override
    public boolean isEmpty() {
        return size==0;
    }
    /*
     *获取队列长度
     */
    @Override
    public int size() {
        return size;
    }
    /*
     *获取队列队首元素
     */
    @Override
    public T getFrontElement() throws Exception {
        if (isEmpty()) {
            throw new RuntimeException("队列什么也没有啦！");
        }else {
            return queueVals[front];
        }
    }
}

  • 链表实现自定义队列
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
public class CustomLinkedQueue<T> implements CustomQueue<T> {
    private Node front;
    private Node rear;
    private int size;

    public CustomLinkedQueue(){
        //初始化时设置首尾节点都为空
        front = rear =null;
        //初始化节点数为0
        size = 0;
    }
    /*
     * 添加新节点到尾部
     */
    @Override
    public void put(T data) throws Exception {
        Node newNode = new Node(data, null);
        if (isEmpty()) {
            front = newNode;
            //将新节点设置为尾节点
            rear = newNode;
        }else {
            //尾节点后面添加新节点
            rear.nextNode = newNode;
            //将新节点设置为尾节点
            rear = newNode;
        }
        size++;
    }
    /*
     * 移除队首元素
     */
    @Override
    public T remove() throws Exception {
        T object = null;
        if (isEmpty()) {
            throw new RuntimeException("队列是空的哟!");
        }else {
            //保存队首元素值
            object = front.data;
            //将下一节点设置为队首节点
            front =front.nextNode;
        }
        size--;
        return object;
    }
    /*
     * 判断队列是否为空
     */
    @Override
    public boolean isEmpty() {
        return size==0;
    }
    /*
     * 返回队列的长度
     */
    @Override
    public int size() {


        return size;
    }
    /*
     * 返回队列首节点数据
     */
    @Override
    public T getFrontElement() throws Exception {
        return front.data;
    }
    /**
     * 节点内部类
     */
    class Node {
        T data;
        Node nextNode;
        /*
         * 头节点构造方法
         */
        public Node(Node nextNode){
            this.nextNode =nextNode;
        }
        /*
         * 其他节点构造方法
         */
        public Node(T data,Node nextNode){
            this.data=data;
            this.nextNode =nextNode;
        }
    }
}

栈

特点：后进先出(LIFO/last in first out),就像一个箱子，先放进去的东西在底部，需要先拿出上面的东西，下面的东西才能拿出来
使用场景：实现递归以及表达式计算

  • 数组实现自定义栈

(1)自定义栈接口CustomStack.java

1
2
3
4
5
6
7
8
9
10
11
12
public interface CustomStack<T> {
    //压栈方法
    public void push(T data)throws Exception;
    //弹栈/移除顶部元素，并返回对应的数据
    public T pop()throws Exception;
    //获取stact第一个元素
    public T peek();
    //判断栈是否为空
    public boolean empty();
    //返回栈中元素的个数
    public int size();
}

(2)数组自定义栈类CustomArrayStack.java，也可以使用LinkedList集合实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
public class CustomArrayStack<T> implements CustomStack<T> {
    static final int defaultSize = 15;
    //指示顶部元素的位置
    private int size;
    private T[] arrays;
    /*
     *无参构造方法，做一些初始化的操作
     */
    @SuppressWarnings("unchecked")
    public CustomArrayStack() {
        size = 0;
        arrays = (T[]) new Object[defaultSize];
    }
    /*
     *根据用户自定义数组大小初始化数组
     */
    @SuppressWarnings("unchecked")
    public CustomArrayStack(int customSize) {
        size = 0;
        arrays = (T[]) new Object[customSize];
    }
    /*
     *向栈顶添加元素
     */
    @Override
    public void push(T data) throws Exception {
        if (size<arrays.length) {
            arrays[size] = data;
            size++;
        }else {
            throw new Exception("数组栈已经满啦!");
        }
    }
    /*
     *将栈顶的元素移除
     */
    @Override
    public T pop() throws Exception {
        T topData;
        if (empty()) {
            throw new Exception("数组栈为空!");
        }else {
            topData = arrays[size-1];
            size--;
        }
        return topData;
    }
    /*
     *获取栈顶的元素
     */
    @Override
    public T peek() {
        return arrays[size-1];
    }
    /*
     *判断栈是否为空
     */
    @Override
    public boolean empty() {
        return size==0;
    }
    /*
     *返回栈的长度
     */
    @Override
    public int size() {
        return size;
    }
}

  • 链表实现自定义栈
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
public class CustomLinkedStack<T> implements CustomStack<T> {
    private int size;
    private Node topNode;
    @Override
    public void push(T data) throws Exception {
        Node newTopNode;
        if (empty()) {
            newTopNode = new Node(data, null);
        }else {
            newTopNode = new Node(data, topNode);
        }
        topNode = newTopNode;
        size++;
    }
    @Override
    public T pop() throws Exception {
        Node oldTopNode = topNode;
        topNode = topNode.nextNode;
        size--;
        return oldTopNode.data;
    }
    @Override
    public T peek() {
        return topNode.data;
    }
    @Override
    public boolean empty() {
        return size==0;
    }
    @Override
    public int size() {
        return size;
    }
    /**     * 节点内部类
     */
    class Node{
        private T data;
        private Node nextNode;
        public Node(T data,Node nextNode){
            this.data = data;
            this.nextNode = nextNode;
        }
    }
}

链表

特点：存储可以不连贯，根据索引将数据联系起来，当查询元素的时候需要从开头开始去查询，所以效率比较低，然而增加或删除元素的时候只需要修改索引就可以了。
使用场景：少查询，需要频繁插入或删除的情况
链表具有逻辑连续，物理存储不连续且大小不固定的特点，它是基于指针实现的。其中单链表和单向循环链表中的每一个节点包含了一个数据域和一个指针域，数据域保存节点的数据，指针域保存节点的下一个节点位置，当需要查找当前节点的下一个节点时，即可通过指针域保存的位置信息，定位下一节点。而其中双向循环链表这包含两个指针域和一个数据域，两个指针与分别表示前一节点的位置和下一节点的位置
(1)单链表

(2)单向循环链表

(3)双向循环链表

数组与链表的区别

(1)数组连续，链表不连续
(2)数组内存静态分配，链表内存动态分配
(3)数组查询时间复杂度为O(1),链表为0(n)
(4)数组增加删除的时间复杂度为O(n),链表为O(1)
(5)数组从栈中分配空间，链表从堆中分配空间

本文标题:基础数据结构分析汇总

文章作者:北京大医同盟-技术部

发布时间:2018年05月27日 - 11时46分

最后更新:2018年05月28日 - 15时00分

原始链接:http://blog.cnlod.com/2018/05/27/java-data-structure/

许可协议: "署名-非商用-相同方式共享 3.0" 转载请保留原文链接及作者。

文章目录
  1. 1. 数据结构与算法学习大纲
    1. 1.1. 数组
    2. 1.2. 队列
    3. 1.3. 栈
    4. 1.4. 链表
  2. 2. 数组与链表的区别